Unos investigadores de la Universidad Complutense de Madrid han creado el primer ejemplo de procesador que utiliza un nuevo tipo de números para computación, llamados posits. Este formato, que se añade al de los números enteros y de coma flotante usados habitualmente, se puede emplear en la aritmética de los cálculos científicos y, especialmente, en el campo del aprendizaje automático y la inteligencia artificial. El trabajo, titulado Open-source posit RISC-V core with quire capability, se refiere a una implementación de código abierto para procesadores RISC-V; el trabajo original de Gustafson y Yonemoto donde se describen matemáticamente los posits se publicó hace algunos años como Beating Floating Point at its Own Game: Posit Arithmetic [PDF] (Aritmética posit: cómo batir a la coma flotante en su propio juego).
Para entender la relevancia hay que entender cómo son los otros dos tipos de números habituales en informática: los enteros y los de coma flotante y qué ventaja suponen lo posits ante lo que actualmente hacer funcionar a los procesadores más potentes.
Cuestión de bits
Cuando un ordenador trabaja con números enteros (0, 1, 2, 27, 12765, -42…) estos números se convierten de su valor decimal a su representación en binario. Por esta razón, cuanto más grande (o pequeño) sea el número más bits necesita, aunque en la práctica se emplean tamaños fijos (8, 32, 64 bits…) para simplificar las cosas. En 8 bits pueden almacenarse 28 o 256 valores, que se suelen interpretar como los números del 0 al 255 o bien del -127 al 128. Si se quieren usar números negativos se utiliza uno de los bits (que puede tomar el valor 0 ó 1) para indicar el signo. Con 16 bits se pueden representar 65536 valores, con 32 bits más de 4.000 millones, etcétera.
Pero el formato de los enteros, ya sean positivos o negativos, no permite representar números reales (que incluyen los fraccionarios o «valores con decimales»). En los ejemplos anteriores estarían el 3 y el 4, pero no se podría representar el 3,14 o el 2050,7. Para esto hay que utilizar otra idea; el llamado formato de coma flotante.
Al usar coma flotante los números pasan a representarse de otra forma: una mantisa (o coeficiente) y un exponente (en cierta base, normalmente 2); el exponente viene a determinar dónde se sitúa esa coma que «flota» por ahí. Hay diversos formatos de coma flotante, pero el estándar IEEE 754 define el más común. Es algo similar a la representación científica en forma 6,022 × 1023; aquí 6,022 sería la mantisa o coeficiente (un número real con una coma y decimales) y el 23 el exponente. De este modo en los números de coma flotante de 32 bits se usan 23 bits como coeficiente, 8 como exponente y 1 como signo. En este estándar se pueden representar números tan grandes como 10127 o tan minúsculos como 10126, aunque entre los más pequeños haya ciertos «saltos».
Esos «saltos» en la precisión tienen que ver que en las conversiones entre decimal y binario de números fraccionarios la equivalencia no es siempre exacta; por ejemplo 0,1 se representa en binario como 0.00011001100110011001100… pero hay que cortar en algún punto, dependiendo de los bits disponibles. Al reconvertirlos a decimal pueden aparecer errores, y al evaluar una fórmula puede incluso suceder que 0,1 + 0,1 + 0,1 no equivalga a 0,3 en algunos lenguajes de programación, lo cual es un problema. Mediante redondeos, o usando una mayor precisión (doble precisión, cuádruple precisión, óctuple precisión…) se pueden minimizar estos problemas, pero a costa de más necesidades de cálculos y memoria.
Los posits, mejores números
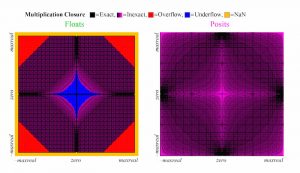En la representación numérica posit la idea es apostar por una precisión que podría considerarse más «práctica» para ciertas tareas, en especial las más modernas. Una curiosidad de este formato es que permite sacrificar bits de la mantisa en pos de la precisión, para minimizar los problemas de redondeo. Lo que se usa además de la mantisa, el exponente y el signo, es un valor llamado régimen, de tamaño variable (a partir de 2 bits) y que viene a simbolizar –por explicarlo llanamente– lo preciso que se desea que sea el número. Si se necesita poca precisión porque los números son enteros o pequeños se puede usar un régimen de 2 bits y dejar más precisión para el coeficiente. En cambio si se requiere una precisión milimétrica se utiliza un régimen más grande con menos bits para el exponente.
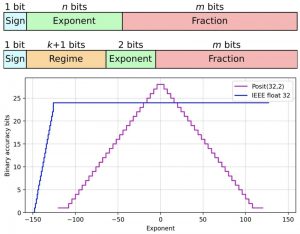El resultado es un estándar de representación numérica que resulta especialmente práctico para aplicaciones reales y modernas como la inteligencia artificial y sus aplicaciones prácticas. En los cálculos de las redes neuronales es normal tener que multiplicar reiteradas veces valores de coma flotante; al hacerlo se acumulan los pequeños errores, se pierde algo de información y el resultado tiende a ser válido pero menos preciso de lo deseable. Utilizando posits se pueden llevar a cabo esos mismos cálculos con mayor exactitud dado que no son valores necesariamente muy grandes o pequeños, simplemente requieren más decimales.
El resultado es un formato más práctico y con el que se pueden realizar mejores cálculos sin sacrificar la velocidad de cálculo. Los investigadores han propuesto no sólo que se utilice como estándar más allá del IEEE 754 sino que también han comprobado empíricamente en un chip FPGA, algo palpable, la velocidad de los cálculos con valores de 32 bits en ambos formatos. El resultado son cálculos mil veces más precisos en la multiplicación de matrices, uno de los cálculos habituales que se realizan en redes neuronales. Así que parece que los posits son, y no necesariamente bit arriba, bit abajo, sino por mucho, bastante mejores que los números de coma flotante habituales.
